티스토리 뷰
728x90
반응형
오늘은 파이썬으로 지도학습 중 하나인 회귀를 공부한 것을 정리해보았다.
순서
- 임의의 데이터 및 해당 데이터 그래프 생성
- 제곱오차함수
- 경사 하강법
- 최종 그래프 출력
임의의 데이터 및 해당 데이터 그래프 생성
import numpy as np
import matplotlib.pyplot as plt
#데이터 생성
np.random.seed(seed=1)
X_min = 4
X_max = 30
X_n = 16
X = 5+25*np.random.rand(X_n)
Prm_C = [170, 108, 0.2]
T = Prm_C[0] - Prm_C[1]*np.exp(-Prm_C[2]*X) + 4*np.random.rand(X_n)
plt.figure(figsize=(5,5))
plt.scatter(X,T)
plt.xlim(X_min,X_max)
plt.grid(True)
위 코드는 임의의 데이터를 생성하는 코드이다.
x 축의 범위는 4~30이며 데이터 개수(X_n)은 16개이다.
X는 x 축의 키, T 는 y축의 키이다.
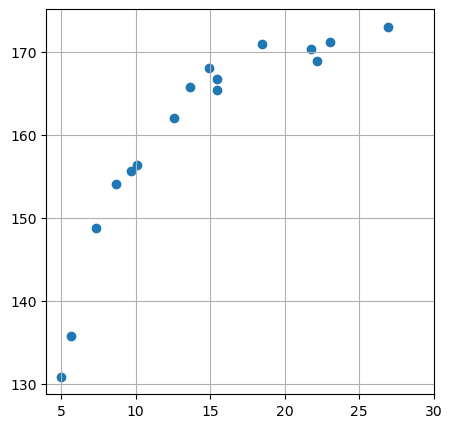
이렇게 데이터가 불균형하게 분포되어 있다. 여기에 일직선을 그리면 해당 데이터가 없는 부분도 값을 예측해볼 수 있다.
일직선을 구하는 방법은 가상의 일직선을 그려서 일직선과 점들과의 거리가 최소가 되도록 해준다.
직선 방정식은 아래와 같은데
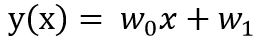
w0과 w1에 적당한 값을 넣으면 다양한 위치와 기울기의 직선을 만들 수 있다.
가상의 직선(yn)과 점(tn)의 차를 구하는 공식은 아래와 같다. 아래 공식은 제곱 오차 함수이라고 한다.

여기에 J는 평균 제곱 오차이다.
제곱오차함수
def mse_line(x,t,w):
y = w[0]*x+w[1]
mse = np.mean((y-t)**2)
return mseJ가 가장 작아지는 w0과 w1은 경사 하강법으로 구하면 된다.
경사 하강법은 아래와 같이 구하면 된다.
경사 하강법은 함수의 기울기를 구하여 기울기가 낮은 쪽으로 계속 이동시켜 극값에 이를 때까지 반복시키는 방법이다.
경사 하강법
def dmse_line(x,t,w):
y = w[0]*x+w[1]
d_w0 = 2*np.mean((y-t)*x)
d_w1 = 2*np.mean(y-t)
return d_w0, d_w1
def fit_line_num(x,t):
w_init=[10.0,165.0]
alpha = 0.001 #lre
i_max = 100000
eps = 0.1 #반복을 종료 기울기의 절대값의 한계
w_i = np.zeros([i_max,2])
w_i[0,:] = w_init
for i in range(1, i_max):
dmse = dmse_line(x,t,w_i[i-1])
w_i[i,0] = w_i[i-1,0] - alpha*dmse[0]
w_i[i,1] = w_i[i-1,1] - alpha*dmse[1]
if(max(np.absolute(dmse))<eps):
break
w0 = w_i[i,0]
w1 = w_i[i,1]
w_i = w_i[:i,:]
return w0, w1, dmse, w_i
W0, W1, dMSE, W_history = fit_line_num(X,T)
dmse_line 함수는 yn의 값의 기울기를 계산하는 함수이다.
기울기가 eps 값에 도달하면 fit_line_num 함수는 그만둔다.
최종 그래프 출력
def show_line(w):
xb = np.linspace(X_min, X_max, 100)
y = w[0]*xb+w[1]
plt.plot(xb,y,color=(.5,.5,.5),linewidth=4 )
#그래프 생성 및 그래프 꾸미기
plt.figure(figsize=(4,4))
W = np.array([W0,W1])
mse=mse_line(X,T,W)
print(f'w0={W0:.3f}, w1={W1:.3f}')
print(f'SD={np.sqrt(mse):.3f} cm')
show_line(W)
plt.plot(X,T,marker='o', linestyle='None',color='cornflowerblue',markeredgecolor='black')
plt.xlim(X_min, X_max)
plt.grid(True)
plt.show()
이렇게 그래프에 각 점들 거리의 최소 값의 직선이 그려졌다. 이렇게 되면 임의의 x 값을 넣어도 y 값을 예측할 수 있게 되었다.
출처
- (책) 파이썬으로 배우는 머신러닝 교과서
728x90
반응형
250x250
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
링크
TAG
- Linux
- 라즈베리파이
- tailwind
- NestJS
- Til
- CSS
- 재미있는
- Kernel
- opencv
- 자바스크립트
- raspberrypi
- JSON
- 모닝독서
- Python
- C
- SQL
- tailwindcss
- variable
- 포인터
- JS
- var
- QT
- 20.03.11.(목)
- 초아
- 미라클모닝
- JavaScript
- 오늘의 공부
- yocto
- js syntax
- 스타벅스
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
글 보관함
